参考:阮一峰
问题:在字符串S = "BBC ABCDAB ABCDABCDABDE"中查询是否存在P = "ABCDABD"
按照字符串匹配的步骤可以得到这个中间步骤:
到了这一步,按照暴力算法,是将搜索词整个后移一位,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把"搜索位置"移到已经比较过的位置,重比一遍。如下:
那么换一个思路,不把搜索位置移动回去,而是移动搜索词,让搜索位置可以继续往后移动,这样的效率会高很多。这也是KMP算法的思路:
那么问题就转变成了怎么确定搜索词的移动距离
讨论这个问题,要先知道几个概念:
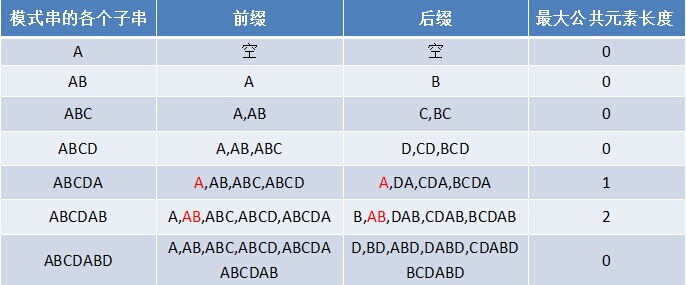
1 2 3 4 5 6 7 8 9 10 11 12 13 前缀:除了最后一个字符以外,该字符串的全部头部组合 后缀:除了第一个字符以外,该字符串的全部尾部组合 部分匹配表:一个字符串的前缀和后缀的最长公有元素的长度 i : 数组的下标 ne[i] : 以i为结尾的部分匹配的值,ne数组即为部分匹配表。有性质:ne[1] = 0, ne[i] < i ne[i] = j 含义:以 i 为结尾长度为 j 的字符串等于从1开始长度为 j 的字符串, 即p[1 ~ j] == p[i - j + 1 ~ i], 即以i为结尾的子串的最大公共元素长度为j,j即为最大公共元素长度
来看字符串ABCDABD
那么可以得到下面这张表:
P[]
A
B
C
D
A
B
D
i
1
2
3
4
5
6
7
ne[i]
0
0
0
0
1
2
0
"部分匹配"的实质是,有时候,字符串头部和尾部会有重复。比如,“ABCDAB"之中有两个"AB”,那么它的"部分匹配值"就是2("AB"的长度)。搜索词移动的时候,第一个"AB"向后移动4位(字符串长度-部分匹配值),就可以来到第二个"AB"的位置。
接下来具体看看ne数组怎么求:(类似于对自己做KMP匹配)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 for (int i = 2 , j = 0 ; i <= m; i++) { while (j && p[i] != p[j + 1 ]) j = ne[j]; if (p[i] == p[j + 1 ]) { j++; ne[i] = j; } else ne[i] = 0 ; } 用上面的例子来模拟一遍求ne的过程: A B C D A B D (ne[1 ]默认为0 ) i = 2 时,字母为B,j == 0 ,尝试匹配共有共有元素为1 (j = 0 + 1 )的情况,得到p[i] != p[j + 1 ],执行(3 )同字母C,D i = 5 ,字母A,j == 0 ,尝试匹配j = 0 + 1 ,得到p[i] == p[j + 1 ],执行(2 ) 同字母B 最后匹配字母D,执行(1 ),j = ne[j],之前j == 2 ,执行之后j = 0 ,来看看这个语句字母理解: ne:0 0 0 0 1 2 A B C D A B|D| ---> A B C D A B|D| A B|C|D A B D |A|B C D A B D 匹配失败,按照KMP算法,往后移动p串,原本j == 2 ,而ne[j] = 0 (前两个字母的最大公共元素长度为0 ),所以移动之后j == 0
接下来就是做匹配的过程:(一样的做法)
1 2 3 4 5 6 7 8 for (int i = 1 , j = 0 ; i <= n; i++) { while (j && s[i] != p[j + 1 ]) j = ne[j]; if (s[i] == p[j + 1 ]) j++; if (j == m) { j = ne[j]; } }
简单优化一下求ne的算法,可以得到模板:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 for (int i = 2 , j = 0 ; i <= m; i++ ) { while (j && p[i] != p[j + 1 ]) j = ne[j]; if (p[i] == p[j + 1 ]) j++ ; ne[i] = j; } for (int i = 1 , j = 0 ; i <= n; i ++ ) { while (j && s[i] != p[j + 1 ]) j = ne[j]; if (s[i] == p[j + 1 ]) j ++ ; if (j == m) { j = ne[j]; } }
来源:AcWing
给定一个模式串S,以及一个模板串P,所有字符串中只包含大小写英文字母以及阿拉伯数字。
模板串P在模式串S中多次作为子串出现。
求出模板串P在模式串S中所有出现的位置的起始下标。
第一行输入整数N,表示字符串P的长度。
第二行输入字符串P。
第三行输入整数M,表示字符串S的长度。
第四行输入字符串S。
共一行,输出所有出现位置的起始下标(下标从0开始计数),整数之间用空格隔开。
1≤N≤105 6
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 #include <iostream> using namespace std ;const int N = 10010 , M = 100010 ;int n, m;int ne[N];char s[M], p[N];int main () cin >> n >> p + 1 >> m >> s + 1 ; for (int i = 2 , j = 0 ; i <= n; i ++) { while (j && p[i] != p[j + 1 ]) j = ne[j]; if (p[i] == p[j + 1 ]) j++; ne[i] = j; } for (int i = 1 , j = 0 ; i <= m; i ++) { while (j && s[i] != p[j + 1 ]) j = ne[j]; if (s[i] == p[j + 1 ]) j++; if (j == n) { printf ("%d " , i - n); j = ne[j]; } } return 0 ; }